Wyjątkowo użyteczne drzewo – kilka słów o Merkle tree

Przemek/ 14 listopada, 2022

W blockchainie weryfikacja poprawności danych to jedna z ważniejszych kwestii. Jednak ze względu na sporą liczbę danych może to być czasem problematyczne. Na szczęście istnieje bardzo sprytny mechanizm, który ułatwia całą sprawę, a konkretnie mowa o tzw. Merkle tree.

Dzisiaj dowiesz się, czym to rozwiązanie jest, do czego można je wykorzystać, a na końcu znajdziesz krótki kod w Solidity, który demonstruje jego użycie.

Sadzimy drzewo

Ponieważ dzisiaj będzie mowa o drzewach, to na początek kilka słów dla osób, które nie mają na co dzień do czynienia z branżą IT. Jak możesz się domyślać, nie będę tutaj opowiadał o kawałkach drewna. W informatyce drzewa to struktury danych, dzięki którym w prosty sposób można np. przeszukiwać duże zbiory informacji. Nazwa pochodzi od ich wizualizacji, która wygląda jak odwrócone drzewo, gdzie na górze znajduje się korzeń (ang. root), a na samym dole liście. Przykładem danych, które mogą być przedstawione w formie drzewa, może być struktura Twoich folderów na komputerze. Typów drzew w informatyce znajdziesz bardzo dużo, a każde z nich posiada różne właściwości. Ale dzisiaj skupię się na tym, które znalazło zastosowanie w blockchainie, chociaż może być również używane w innych miejscach.

Merkle tree, bo o nim dzisiaj mowa, nazywane jest również jako drzewo skrótów lub drzewo haszujące. Nazwa pochodzi od nazwiska twórcy (Ralph Merkle), ale również od funkcji haszującej (funkcji skrótu), na której opiera się całe rozwiązanie. Jeżeli jeszcze nie wiesz, czym jest wspomniana funkcja, to zajrzyj do jednego z pierwszych wpisów na moim blogu, w którym znajdziesz szczegółowe wyjaśnienie. Dla przypomnienia powiem tylko w tym miejscu, że dzięki niej z danych wejściowych otrzymujemy ciąg “losowych” danych wyjściowych, które reprezentują wprowadzone informacje. Z samego hasza nie da się wywnioskować, co zostało wrzucone do funkcji, ale dzięki temu, że metoda ta jest bardzo szybka, to możemy zahaszować jakieś dane i porównać oba wyniki, co da nam wiedzę, czy początkowe informacje były identyczne czy też nie.

Merkle tree zbudowane jest w oparciu o drzewo binarne, czyli w skrócie, taki twór, gdzie każdy węzeł ma co najwyżej dwójkę dzieci i jedno z nich jest prawą, a drugie lewą odnogą.

W odróżnieniu od większości drzew, budowę Merkle tree rozpoczyna się od liści, a nie od korzenia. Na początku potrzebujemy zgromadzić ciąg danych, które będziemy chcieli umieścić w drzewie. 

Załóżmy, że byłyby to cyfry:
1,2,3,4,5,6,7,8

Każdą z liczb przepuszczamy przez funkcję haszującą, a następnie jej rezultat umieszczamy jako liść drzewa. Po tej operacji bierzemy po dwa sąsiadujące ze sobą wyniki i z nich również tworzymy hasz, który staje się ich rodzicem. Całość powtarzamy aż do momentu, gdy z otrzymanych wyników otrzymamy ostateczny wynik, który umieszczamy jako korzeń, nazywany w tym przypadku mianem Merkle root. Poniżej znajduje się grafika prezentująca gotowe drzewo.

W powyższym przykładzie liczba początkowych danych pozwoli w łatwy sposób stworzyć idealne drzewo, jednak prawdopodobnie częściej będziemy mieć do czynienia z nieco inną sytuacją. Rozważmy teraz sytuację, gdy nasz ciąg wejściowy składa się z siedmiu cyfr:

1,2,3,4,5,6,7

W takim wypadku stosuje się uzupełnienie, polegające na przekopiowaniu poprzedniej wartości. W tym wypadku brakuje nam tylko jednej danej, ale działa to dokładnie tak samo w innych sytuacjach. Ostateczny wynik będzie wyglądał następująco:

Korzeń prawdy

Dzięki tak zbudowanemu drzewu możemy w bardzo prosty i wydajny sposób sprawdzić, czy konkretna dana znajduje się w naszym zbiorze. Dla przykładu: chcielibyśmy udowodnić, że liczba 5 faktycznie występuje w tym ciągu. Zanim wytłumaczę, jak to zrobić z użyciem Merkle tree, zastanówmy się, jakbyśmy tego dokonali bez niego. Rozwiązanie jest banalne, ponieważ wystarczyłoby przejść przez cały ciąg i porównywać każdy element z tym poszukiwanym. Nie stanowi to problemu, gdy nasz zbiór jest mały, ale przy ogromnej liczbie danych, będzie to bardzo niewydajne rozwiązanie. Tutaj przychodzą nam na pomoc właściwości zbudowanego drzewa.

Jak już wiesz, najdrobniejsza zmiana danych wejściowych funkcji haszującej, sprawia, że jej wynik jest całkowicie inny. Skoro Merkle tree w całości generowane jest na podstawie haszy, to jedyne co musimy zrobić, to udowodnić, że hasz poszukiwanej danej znajduje się w drzewie. Wykorzystując do tego fakt, że Merkle root bazuje na wszystkich haszach z drzewa i najdrobniejsza zmiana jednego z nich będzie miała wpływ na sam korzeń, możemy bardzo uprościć cały proces weryfikacji.

W takim wypadku zamiast przeszukiwać zbiór składający się z 8 wartości, wystarczy, że dostarczymy ich cztery (pięć, wliczając Merkle root), ponieważ przy ich pomocy możemy w prosty sposób wyliczyć ostateczny hasz. Jeżeli będzie on zgodny z tym, przechowywanym przez Merkle root, oznacza to, że dana wartość występuje w drzewie.

Może i przy zbiorze 8 elementowym oszczędność nie jest wielka, ale dla zbioru składającego się z 1000 danych wystarczy, że znamy jedynie 10 haszy i w ten sposób możemy sprawdzić, czy poszukiwana wartość znajduje się w drzewie.

Zastosowanie

Merkle tree nie musi być wykorzystywane w blockchainie, ale na pewno tutaj znalazło wiele zastosowań. Pierwsze i chyba najbardziej oczywiste z nich jest związane z weryfikacją transakcji. Dzięki drzewom skrótu w łatwy sposób jesteśmy w stanie sprawdzić, czy dana transakcja zawarta jest w konkretnym bloku. Poniżej znajduje się zrzut ekranu ze strony blockchain.com, na którym znajdziesz dane dotyczące jednego z bloków Bitcoina. Jak widzisz, zapisany jest w nim Merkle root, który zawiera w sobie informacje o wszystkich powiązanych transakcjach. Każdy blok zawiera średnio od 1500-2000 transakcji, a dzięki Merkle tree udowodnienie, że któraś z nich została faktycznie w nim zawarta, jest dziecinnie proste i szybkie.

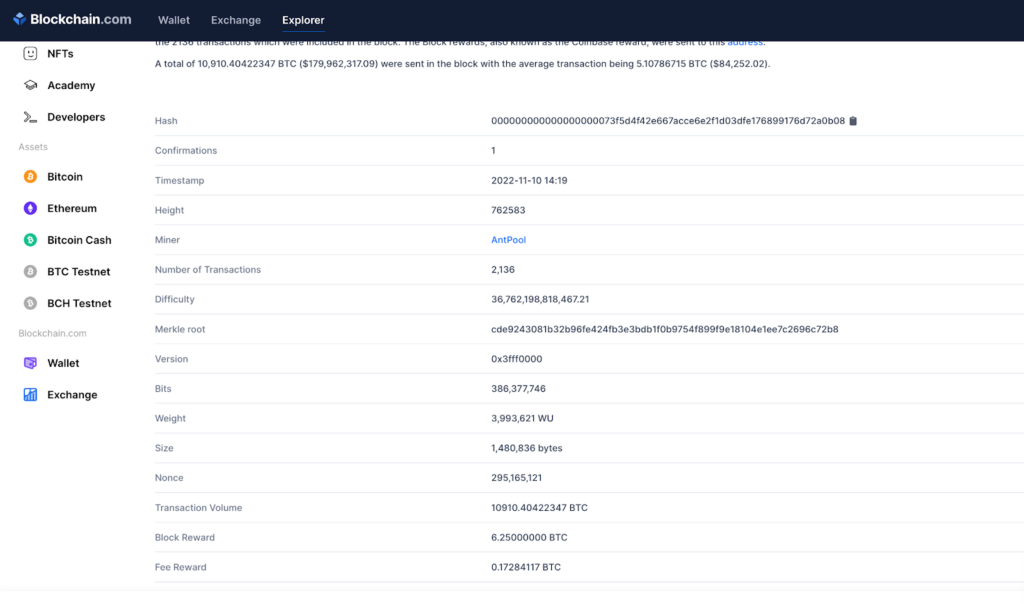
W przypadku Ethereum sprawa wygląda podobnie, jednak Merkle tree służy do weryfikacji całego stanu. Ponieważ w przypadku tego blockchaina mamy do czynienia nie tylko z prostym transferem środków między adresami, ale również z różnego rodzaju logiką zawartą w smart kontraktach. Stąd drzewo wykorzystywana do przechowywania tych informacji jest bardziej skomplikowane i nosi nazwę Patricia Merkle Trie (tak trie, a nie tree jak poprzednio:), ale również bazuje na podobnych mechanizmie.

Ale w przypadku rozwiązań blockchainowych nie musimy się ograniczać jedynie do weryfikacji transakcji. Kolejnym ciekawym zastosowaniem jest tworzenie różnego rodzaju whitelisty używanej np. podczas airdropów tokenów. Dla osób niewtajemniczonych airdrop to po prostu rozdanie kryptowalut np. dla użytkowników danego protokołu. Oczywiście można by to zrobić bez użycia Merkle tree, ale byłoby to niezmiernie kosztowne. Z takim przypadkiem musiał się zmierzyć w przeszłości Uniswap, kiedy zapragnął rozdać swoje tokeny jako nagrodę dla aktywnych użytkowników.

Mogli do tego podejść na kilka sposobów. Jednym z nich byłoby zapisanie na blockchainie wszystkich adresów, które mogłyby odebrać tokeny. Jednak ten sposób byłby strasznie kosztowny dla Uniswapa, ponieważ ich liczba była bardzo duża. Na szczęście ktoś w ich zespole znał się na rzeczy i wykorzystano do tego Merkle tree. Na blockchainie wystarczyło zapisać jedynie wartość Merkle root, a każdy użytkownik, który zgłaszał się po odbiór tokenów, musiał jedynie wywołać funkcję, do której dołączane były odpowiednie węzły z drzewa. Tym sposobem Uniswap zaoszczędził ogromne pieniądze.

Zastosowań Merkle tree jest bardzo dużo i nie muszą one być wykorzystywane jedynie przez rozwiązania blockchainowe. GitHub jest tutaj dobrym wzorem, który również używa tej struktury danych.

Jeszcze innym przykładem mogą być rozproszone systemy do przechowywania plików. Przy pomocy Merkle tree można w nich w łatwy sposób sprawdzić, czy część pliku, którą chcemy pobrać z danego węzła, jest faktycznie jego częścią.

Zastosowania można by mnożyć i mnożyć, dlatego na tych skończę i przejdę na koniec do kawałka kodu, który zademonstruje w praktyce, jak można wykorzystać Merkle tree.

Weryfikacja w praktyce

Nie będę zajmował się budowaniem samego drzewa. Jednak jeżeli masz na to ochotę, to możesz do tego wykorzystać jedną z gotowych bibliotek, którą znajdziesz np. tutaj. Ja skupię się jedynie na kodzie smart kontraktu, który pozwoli sprawdzić, czy odpytujący adres znajduje się na uprawnionej liście.

pragma solidity 0.8.17;
 
import "https://github.com/OpenZeppelin/openzeppelin-contracts/blob/master/contracts/utils/cryptography/MerkleProof.sol";
 
contract MerkleExample {
   bytes32 public merkleRoot;
 
   constructor(bytes32 _merkleRoot) {
       merkleRoot = _merkleRoot;
   }
 
   function areYouEligible(bytes32[] calldata _merkleProof) external view returns(bool) {
       bytes32 leaf = keccak256(abi.encodePacked(msg.sender));
       return MerkleProof.verify(_merkleProof, merkleRoot, leaf);
   }
}

Jak widzisz kodu jest bardzo mało, a to głównie za sprawą użycia gotowego rozwiązania dostarczonego przez OpenZeppelin (nie ma co wymyślać koła na nowo). Jeżeli chcesz zagłębić się w tajniki ich rozwiązania, to możesz to zrobić tutaj.

Nasz kontrakt przechowuje jedną wartość, jaką jest Merkle root. Podawany jest on podczas tworzenia kontraktu i nigdy nie będzie mógł być zmieniony. Daje to pewność, że nikt nie zmieni listy uprawnionych osób. Metoda areYouElibile przyjmuje jeden parametr, jakim jest Merkle proof, czyli innymi słowy lista zawierająca wszystkie węzły niezbędne do weryfikacji. Podane one muszą być w odpowiedniej kolejności. Patrząc na drzewo, można powiedzieć, że bierzemy najpierw odpowiednie liście idąc od lewej strony, po czym powtarzamy tę czynność na każdym poziomie. Odnosząc to do wcześniejszego przykładu z liczbami Merkle proof wyglądałby następująco:

[h6, h12, h13]

Tak jak wspomniałem, nie będziemy sami zajmowali się implementacją drzewa, dlatego do wygenerowania Merkle root oraz proof możemy skorzystać np. z tej aplikacji.

Załóżmy, że chcielibyśmy, aby uprawnionymi adresami były:

• 0x5B38Da6a701c568545dCfcB03FcB875f56beddC4
• 0xAb8483F64d9C6d1EcF9b849Ae677dD3315835cb2
• 0x4B20993Bc481177ec7E8f571ceCaE8A9e22C02db
• 0x78731D3Ca6b7E34aC0F824c42a7cC18A495cabaB
• 0x617F2E2fD72FD9D5503197092aC168c91465E7f2,
• 0x17F6AD8Ef982297579C203069C1DbfFE4348c372
• 0x5c6B0f7Bf3E7ce046039Bd8FABdfD3f9F5021678
• 0x03C6FcED478cBbC9a4FAB34eF9f40767739D1Ff7

Dla takiego zbioru Merkle root będzie wyglądał następująco:

0x70b8e8088ae556faa07c4b4c972240935971ff7249949faf0cc1648dff84055b

Możemy teraz wgrać kontrakt i sprawdzić, czy wszystko działa jak należy. Wykorzystamy do tego lokalny blockchain dostarczony przez Remixa. Teraz sprawdźmy, czy adres “0x5B38Da6a701c568545dCfcB03FcB875f56beddC4” jest faktycznie na liście. Żeby to zrobić, musimy wywołać funkcję będąc tym użytkownikiem. Merkle proof generujemy przy użyciu wcześniej wspomnianej aplikacji i wynik wrzucamy do naszej funkcji.

Wygląda na to, że wszystko jest okej – funkcja zwróciła wartość “true”. Wrzućmy jeszcze dla pewności jakiś adres, który nie występował na liście np. “0xdD870fA1b7C4700F2BD7f44238821C26f7392148”. Nie będziemy w stanie wygenerować dla niego Merkle proof, dlatego wykorzystamy ten poprzedni.

Jak można było się spodziewać, tym razem wynik jest negatywny. Musisz też pamiętać, że nawet dla dobrego adresu podanie nieodpowiedniego Merkle proof sprawi, że nie zostanie on odnaleziony w drzewie.

Tym sposobem dotarliśmy do końca dzisiejszego wpisu. Mam nadzieję, że udało mi się wytłumaczyć Ci, czym jest oraz jak działa Merkle tree. Jeżeli pracujesz w świecie IT, to może przyda Ci się ta wiedza w codziennym życiu, a jeśli nie, to przynajmniej będziesz miał świadomość kolejnego rozwiązania wykorzystywanego w wielu blockchainowych projektach. Do zobaczenia za tydzień 🙂